#PreAgebra - Which fraction is bigger? Smaller?

Questions:



We'll be doing 3c, 4c, 5c, 6b, 6c

Answers:

See below:

Analysis:

In all of these questions, we're dealing with what appears to be a bunch of random numbers dividing other rather numbers. It's all quite confusing! But if we work with these numbers, they'll tell us which of them is bigger and which is smaller.

There are a bunch of ways to think of fractions and to understand what they are telling us, but one of my favourites is a pizza pie analogy. All of these questions have three fractions, so let's imagine three pizza pies all the same size. We're going to cut those pies into some number of same sized pieces - it's the denominator, or the bottom number, that tells us how many. Keep in mind that as the number of pieces increases, the size of those pieces drops (if I cut a pizza in half, 1 slice is really big. If I cut that same pizza into 100 pieces, the pieces are really really small).

After we've cut the pizza into the number of pieces we want, then we'll pick out some number of those pieces. It's the numerator, or the top number, that tells us that. Let's start working 3C so you can see what I mean:



That first pizza has been cut into 7 pieces and we'll take 3, the second pizza has been cut into 2 pieces and we'll take 1, and the third pizza has been cut into 5 pieces and we get 3. Ok - so which option gives us the most amount of pizza? Right now it's a little hard to tell, isn't it? The slices are all different sizes and we're taking different amounts. What would really help is if the slices were all the same size - if we cut the pizza into slices that are all the same size - then all we'd need to do is pick the fraction with the largest numerator (the top number).

Now, as we cut the pizza into smaller and smaller slices, we still want to get the same amount of pizza! So as we increase the number of slices, we get more of them.

As an example, look at the  and think about a pizza where it's cut into 2 and you get 1 slice. If we cut the pizza into quarters, so 4 pieces, how many pieces of pizza do you get now? 2. Getting 2 slices when it's cut into 4 is the same as when you get 1 slice when the pizza is cut into 2 (image from chilimath.com):



This is where the idea of a Common Denominator comes into play - and all that means is that we want the bottom numbers to all be the same (so that the pizza slices are all the same size).

So how do we get to the Common Denominator? One way is to simply multiply all the denominators together (this may not get you to the Lowest Common Denominator, which you'll need to find in other questions, but it'll work well here):

7 x 2 x 5 = 70

Ok - so our denominator will be 70.

Now - we need to remember a couple of things at this point. The first is that we can always multiply by the number 1 and end up with the same number we started with. 3 x 1 = 3. I can multiply by 1 and not change the value of the fraction.

The other thing we need to remember is that 1 doesn't always look like 1. If I divide a number by itself, what do I get? 1. And so:



So now we can multiply the different fractions by versions of the number 1 so that we get our denominators to all be 70:







Remember, these are all equivalent to the fractions I had before - all I did is multiply by 1.

Ok - which amount of pizza is most? The one with 42 slices in it. And which fraction was that? 

All the other questions can be worked this same way:

4C



The Common Denominator is 8 x 6 x 3 = 144:





The one with 36 pieces is the smallest, and that is 

5C



The common denominator is 7 x 6 x 5 = 210



And now they can be arranged easily from largest to smallest:



6B

This question has a little twist to it - they include the number 1 as a fraction. Let's change it's look slightly so that it really does look like a fraction:



This says I cut the pizza into 1 piece (or in other words, it's the whole pizza) and I get that one piece (again, the whole pizza).

Now let's work this the same we have the others:



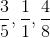
The common denominator is 5 x 1 x 8 = 40:



From smallest to largest, it's the one with 20, then 24, then 40, or:



6C



The common denominator is 7 x 9 x 3 = 189



From smallest to largest it's the one with 27, then 63, then 84, or:



~~~~~

Questions and comments always welcome!